Cinthia Kleiner, Data Scientist – Semantix.
Introduction:
A paradigm in foundation models development involves the extensive initial training on large-scale generic data, followed by tailoring the problem for specific domains or tasks. As the scale up, the feasibility of performing full fine-tuning, which can require retraining all the models parameters, diminishes. For instance, using a model like GPT 3.5 which has 175 billion parameters [1] the fine-tuning process becomes expensive in terms of computation and memory requirements. To address this defiance, Microsoft Researchers introduced Low-Rank-Adaptation or LoRA which stands as an efficient fine-tuning methodology to address the challenges related with the fine-tuning of extensive models [2].
LoRa comes out with a solution through the preservation of the pre-trained model’s weights while there are trainable layers, referred to as rank-decomposition matrices. With this approach, there is a significant reduction in the trainable parameters which leads to reduction in the GPU memory demands for loading it, as it eliminates the need to compute gradients for the majority of the model’s weights, reducing also the computation requirements [3].
Moreover, the landscape of fine-tuning was also transformed by the technique of Quantized Low-Rank Adaptation (QLoRA), a technique that employs advanced strategies to further optimize the memory requirements while maintaining the model performance. By introducing new approaches such as the use of NormalFloat 4 quantization, double quantization and paged optimizers, this technique was capable of enhancing the fine-tuning process, making it more accessible and efficient. This post aims to explore these techniques addressing the challenges of full-fine tuning an extensive model, exploring the role of LoRA and QLoRA techniques and their transformative potential in the realm of the fine-tuning process.
Why Fine-tune a model ?
Fine tuning is the method which aims to retrain the model parameters, adapting it for a target task or domain rather than training a model from scratch. So, in this process, a pre-trained model, which has already learned important features, undergoes further training on a specific and smaller dataset. Figure 01 shows the pipeline of fine-tuning a Large-Language-Model. This approach proves valuable for enhancing the versatility of pre-trained models, aiming to boost their performance in various practical applications [3 – 5].This process can yield significant benefits in particular scenarios, such as:
- Enhanced Task-Specific Performance: Adapting a pre-trained model on a specific task or domain it is capable of refining the model’s knowledge with the intricacies of that application, so the performance on that specific task will be improved [5 – 6].
- Reduced Data Requirements and Training Time: The fine-tuning process requires fewer computation resources, time and data when compared to training a model from scratch
- Enhanced Generalization: With this approach, models improve their generalization capabilities to new data by extracting relevant features from it [5 – 6]. .
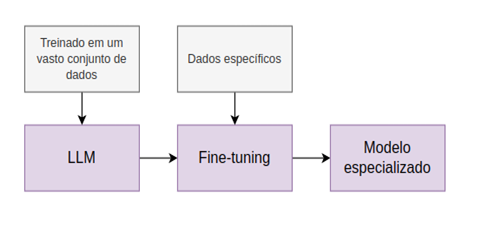
Figura 01: Pipeline for fine-tuning a Large Language Model
The challenges in full fine-tuning:
Especially in the Large Language Models Context, full parameter fine-tuning is a resource-intensive endeavor, demanding substantial computation and memory power to manage with weights and optimizer states. It is important to note that the gradients and optimizer states typically result in a memory footprint 12 times larger than the model itself. Consequently, a field called “Parameter Efficient Fine Tuning” also known as PEFT, has emerged with innovative approaches to deal with these limitations. The methodologies proposed by PEFT are designed to fine-tune a subset of the model parameters. These approaches exemplified by techniques like LoRA and QLoRA are capable not only to minimize the resource consumption but also expedites the training process [7].
Low Rank Adaptation (LoRA):
LoRA is an approach engineered to enhance the accessibility and efficiency of the fine-tuning process. It capitalizes a critical insight: the difference between the model fine-tuned weights for a domain task and the initial pre-trained weights often exhibits “low intrinsic rank”, which means that it can be approximated by a matrix with low-rank [2].
A low rank means that the matrix possesses a limited number of linearly independent columns, so it reduces complexity. Low rank matrices can be expressed as the product of two smaller matrices. This leads to the hypothesis that the difference between fine-tuned and original pre-trained weights can be represented as the matrix-product of two smaller matrices which leads to significant gains on computational efficiency [7, 12, 14].
In this way, in the LoRA framework, the original matrix weight remains static during the fine-tuning process. Insead, two matrices, denoted A and B undergo the process (Figure 02).
output(h) = Input(x)PretrainedWeight(Wo) + Input(x)LowRankUptade(BA)
Equation 01 – Neural Network Adaptation [4]
With Equation 01, it is possible to note that the output of a model is represented by two parts: The first evolves multiplying the input data with the original pre-trained weights of the model, and the second entails the multiplication of the input data with the low-rank approximation (BA). Then, these terms are summed to yield the final output. This adaptation enables LoRA to achieve remarkable savings in storage and memory [4]. When it comes to the final count of trainable parameters in this approach, it depends on the size of the low-rank updated matrices, which is a function of the shape of the original weight’s matrix and the rank chosen in the training process [4].
Applying LoRA on Transformers Architecture:
The LoRA technique can be applied to a specific subset of weight matrices within a neural network in order to reduce the overall number of trainable parameters. In the Transformers architecture, that includes the weight matrices within the self-attention module (Wq, Wk, Wv e Wo), and two within the multi layer perceptron module (MLP), LoRA is conventionally applied in attention blocks for the sake of simplicity and parameter efficiency [2, 3], like shown on Figure 03 . In the original paper, the authors found that with rank=4, when applying LoRA only in the Wq and Wv attention blocks gives the best performance on some benchmarks as WikiSQL and MultiNLI [2].
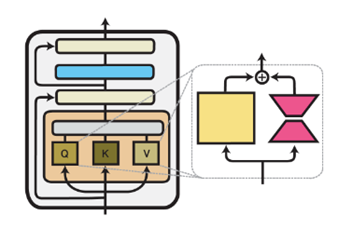
.Figure 03: LoRA applied in attention block in Transformers architecture [17]
LoRA Key Parameters:
When working with LoRA technique, it is important to understand the following parameters.
- Rank (r): Rank it is a measure of how the original weights are decomposed into smaller matrices. This parameter is related to the computational and memory requirements. Lower ranks can enhance the model speed but may come at the cost of performance [9].
- lora_alpha: The scaling of the low-rank approximation. This parameter finetune the tradeoff between the original model and its low-rank approximation. Higher lora_alpha values may amplify the influence of the approximation in the fine-tuning process [9].
- lora_dropout: It is a regulation technique in order to prevent overfitting. Represents the probability of each neuron output being suppressed to zero during the training step [9].
LoRA Advantages:
The LoRA technique has demonstrated notable advantages, including:
- Shared Pre-Trained Model: With LoRA, it is possible to share a pretrained model across multiple tasks. So, it makes it possible to create various LoRA adapters for different purposes [10 – 12].
- Enhanced Training Efficiency: LoRA enhances training efficiency and reduces the hardware barriers. This is achieved by eliminating the need to maintain optimizer states or calculate gradients for most parameters. LoRA focuses on optimizing the injected low rank matrices, streamlining the training process [10 – 12].
- Low Inference Latency: LoRA’s design allows the seamless integration of the trainable matrices with the frozen weights minimizing delays during the deployment [10 – 12].
- Versatility and Compatibility: LoRA is compatible with various methods. For instance, it can be used with techniques such as prefix-tuning. With this compatibility, LoRA becomes a versatile solution for a wide range of applications [2, 11].
Quantized Low-Rank Adaptation (QLoRA):
While LoRa is effective in decreasing storage demands, it is still necessary to use a substantial GPU during LoRA training. This is where QLoRA plays a crucial role [13]. This technique utilizes an innovative high-precision method to quantize a pre-trained model to 4 bits, then it is followed by the incorporation of a compact set of learnable Low-Rank Adapter weights that are tuned with the backpropagation step through the quantized weights [4]. To achieve it, QLoRa introduces a range of innovative strategies aimed at reducing memory consumption while maintaining model performance. These innovations include:
- 4-bit NormalFloat: A quantization data type that is considered as information-theoretically optimal. Particularly suitable for data that follows a normal-distribution. In empirical results, it consistently outperforms 4-bit integers and 4-bit floats [4].
- Double Quantization: A method that quantizes the quantization constants to achieve further memory savings. In this way, double quantization uses the first quantization as inputs for the second quantization. For instance, in a model with 65-billion-parameters it saves almost 3 GB, resulting in average saves of approximately 0.37 bits per parameter [4].
- Paged-Optimizers: Uses unified memory from NVIDIA to avoid spikes during gradient checkpoint when processing batches with long sequence lenght, preventing out-of-memory errors which restricts the fine-tuning of large language models on a single GPU [4].
In summary, QLoRA technique employs a low precision storage data type (4-bit NormalFloat) alongside a computation data type which is (16 bit brain float). The forward and backpropagation passes involve dequantizing the storage data type to the computation data type, so whenever a tensor is utilized, first it is dequantized to BFloat16, followed by performing a matrix multiplication in 16-bit precision. This way, it is possible to note that the weight gradients are only computed using 16-bit BrainFloat [4]. After the computation step, all the weights are back to 4 bits. Figure 04 represents some key differences between QLoRA, LoRA and Full Fine-tuning.
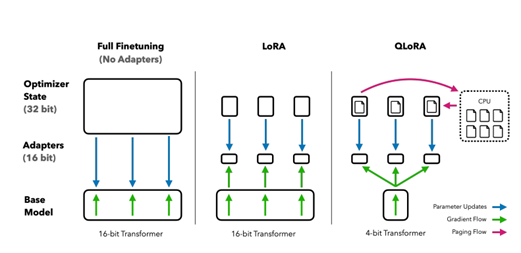
The QLoRA process involves several steps, as presented below:
- Quantization to NF4: The Large Language Model is quantized to 4 bits representation, meaning that the model ‘s matrices are stored in this data type, providing a huge reduction in memory usage [16].
- LoRA training in computation precision: All the computation steps are performed with 16-bit or 32-bit precision. So the model’s weights are temporarily dequantized to the computation precision. Once the computation steps are complete, these elements are reverted to the 4-bit format [16].
- Selective storage in computation precision: In the QLoRA approach, only the LoRA adapters are temporarily stored in the computation precision, while the majority of the model’s weights remain in the 4-bit format. With this strategy, the memory footprint significantly minimizes [13, 16].
Advantages of QLoRA:
QLoRA represents the first method that was capable of fine-tuning a model with 33-billion parameters on a single consumer GPU and 65 billion parameters on a single professional GPU, all of these experiments without compromising performance when compared to a full fine-tuning baseline [4]. The key advantages are present on the following topics:
- Additional Memory Efficiency: By introducing quantization, QLoRA goes a step further in optimizing memory usage, making it especially valuable for deploying large models in devices with limited resources such as edge devices and smartphones [15].
- NormalFloat 4: The QLoRA original paper highlights the performance of NormalFloat4 over standard Float4, demonstrating a significant increase in performance when using NF4 [13].
- Double Quantization: With this technique, it was possible to reduce memory footpŕint while keeping the model’s performance [16].
Conclusions:
The widespread availability of LLM fine-tuning represents more than a technological advancement, it serves as support for innovation across various domains. By increasing the accessibility of fine-tuning LLMs, techniques such as LoRA and QLoRA unlocks opportunities for smaller business, individual researchers and developers. Fine-tuning offers enhanced task specific performance and reduced resource needs. With these techniques, it is possible to leverage advanced models to build solutions that were previously out of reach by fine-tuning.
These techniques are capable of reducing the number of trainable parameters, resulting in lower computational requirements. While fine-tuning is resource intensive, LoRA and QLoRA with their approaches of low-rank adaptation and quantization with NF4 data format are capable of addressing these challenges without compromising performance. These approaches improve training efficiency, reduce hardware barriers and offer versatility in model deployment.
Overall when comparing these techniques, it is possible to note that QLoRA stands out with a good balance between precision and computation efficiency, making a demonstration of a democratic approach for fine-tuning large language models.
References:
[1] https://medium.com/@chudeemmanuel3/gpt-3-5-and-gpt-4-comparison-47d837de2226
[2]HU, Edward J. et al. Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685, 2021.
[3]https://huggingface.co/blog/lora
[4]DETTMERS, Tim et al. Qlora: Efficient finetuning of quantized llms. arXiv preprint arXiv:2305.14314, 2023.
[5]https://medium.com/@prabhuss73/fine-tuning-ai-models-a-guide-c515bcd4b580
[6] https://towardsdatascience.com/fine-tuning-large-language-models-llms-23473d763b91
[8]https://anirbansen2709.medium.com/finetuning-llms-using-lora-77fb02cbbc48
[9] https://deci.ai/blog/fine-tune-llama-2-with-lora-for-question-answering/
[10] https://www.ml6.eu/blogpost/low-rank-adaptation-a-technical-deep-dive
[11] https://www.ikangai.com/lora-vs-fine-tuning-llms/
[12] https://www.analyticsvidhya.com/blog/2023/08/lora-and-qlora/
[16]https://medium.com/@ashkangolgoon/understanding-qlora-lora-fine-tuning-of-llms-65d40316a69b
[17] https://adapterhub.ml/blog/2022/09/updates-in-adapter-transformers-v3-1/




