With the recent progress of Noisy Intermediate-Scale Quantum Technology (NISQ) towards Fault-tolerant Systems – i.e., quantum computers equipped with more efficient error correction systems – we are on the brink of a new era, one where large-scale commercialization of quantum computers becomes a reality.
These quantum computers will not be limited to solving a narrow set of problems but will be applicable to a wide range of tasks. As AI practitioners, we are all wondering over how this technological leap can revolutionize machine learning and, more importantly, lead us towards the realization of Artificial General Intelligence (AGI).
To address this question, we must focus on the most challenging areas in artificial intelligence today, and one such area that stands out is unsupervised/semi-supervised learning of generative models. This area is immensely significant due to the abundance of unlabeled data generated daily, encompassing various forms such as photos, videos, medical images, tweets, financial series, and general text.
In unsupervised generative techniques, the goal is to learn the joint probability distribution P(X,Y). By accurately modeling this joint probability distribution, generative models can effectively capture the statistical dependencies and correlations between observable variables, which are vital in tasks like data generation, imputing missing values, and sampling data distributions.
Oppositive to generative models, discriminative models focus on learning the conditional probability distribution P(Y|X) and are predominantly employed in classification tasks, where the aim is to predict the target variable Y from the observable variable X.
Numerous articles and posts show the disruptive benefits of quantum technologies in artificial intelligence. However, these posts often lack the necessary depth for more technical readers, such as myself and many other data scientists. In this post, I intend to delve into how these two realms, quantum computing and classical AI, can converge to bring tangible advantages through a practical example.
We will discover that this integration is particularly relevant in machine learning scenarios involving optimization of loss functions or modeling complex probability distributions. Quantum computers, especially in hybrid classical/quantum systems, can significantly enhance performance.
My aim is to combine concepts from the classical AI domain, like energy-based AI models, with quantum energy concepts, providing a seamless analogy for this unique combination.
Example: Restricted Boltzmann Machines (RBM)
RBMs are generative models with stochastic hidden layers, i.e., stochastic neurons that model probabilities. They can learn complex probability distributions over high-dimensional data. Such networks have applications as building blocks for speech and image recognition architectures.
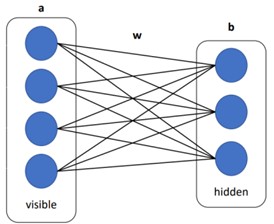
The concept behind these networks draws inspiration from statistical mechanics through the Boltzmann distribution. In this context, we consider a system, like a gas tank, and our aim is to model the total energy of the system based on the various combinations of its particles.
Consequently, we calculate the probabilities for different arrangements of these particles. According to the Boltzmann distribution, the probability of a state i with energy epsilon is expressed as follows:
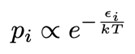
In an RBM, we can calculate the energy value for each combination of input data v and activations h of neurons, where w, a and b are parameters:
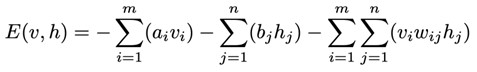
And through the energy value, we can calculate the joint distribution:
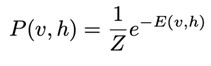
The analogy with statistical mechanics proves to be crucial in modeling this system as a quantum system, since our objective is to identify a configuration with the lowest energy state. This principle lies at the core of quantum annealers.
Now, shifting back to the training of RBMs, we utilize input data v (where v represents the visible layer) to train these neural networks, enabling them to learn the data distribution. Each additional layer we incorporate into these models empowers them to abstractly represent the input data, enhancing the model’s ability to generalize.
However, this comes at the expense of increased complexity in training these networks.
To train a restricted Boltzmann machine, we apply a similar approach to training a neural network, where the loss function of this network is given by the average negative log-likelihood (NLL):
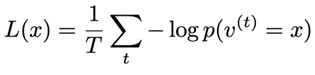
Using gradient descent as the method to search for parameters (W, b, a), we calculate the gradient of the loss function, and we get:
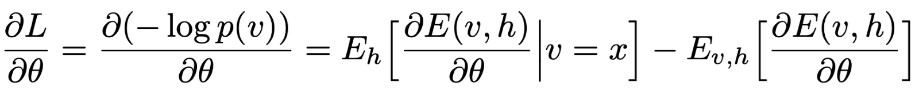
Notably, the first expected value is relatively straightforward to calculate since it relies on the input data v = x. However, the second term requires evaluating the expectation value over 2^N potential configurations of v and h, where N represents the total sum of v and h. This poses a challenging problem due to its exponential growth with N.
This situation contrasts significantly with gradient descent in a standard feedforward neural network, where the terms in the gradient are deterministic functions. Here, we encounter expected values that necessitate sampling from the distribution to compute these values, but representing such distributions proves to be complex.
To address this, Hinton et al. introduced a technique known as Contrastive Divergence (CD), employing Gibbs Sampling to approximate the values of expectations from the unknown joint distribution. However, to calculate the conditional probability of v and h for the Gibbs Sampler iterations, we must assume independence of events.
While CD is an efficient approach, it remains an approximation, introducing inherent errors that can propagate in each step of the gradient descent and may result in poor estimates for (W, b, a). Therefore, we introduce a type of quantum computer called an annealer.
What is Quantum Annealer?
Quantum computers come in various approaches, including those based on trapped ions, topological systems, and a broader category encompassing quantum computers built on quantum gates. However, annealers offer a different approach compared to these traditional systems.
They rely on a fundamental principle of both classical and quantum physics, where every system seeks a configuration with the lowest achievable energy state. For instance, stars take on a spherical shape as this energy configuration represents the lowest among the countless possibilities of their atomic arrangement.
Quantum annealers achieve this through the application of controlled magnetic fields (biases) to an initial qubit configuration, combined with the phenomenon of quantum entanglement. This natural process leads the system to explore configurations of states with the lowest energy, which serves as the solution to optimization problems. As illustrated in the diagram below, we see a final configuration for a 2-qubit system.
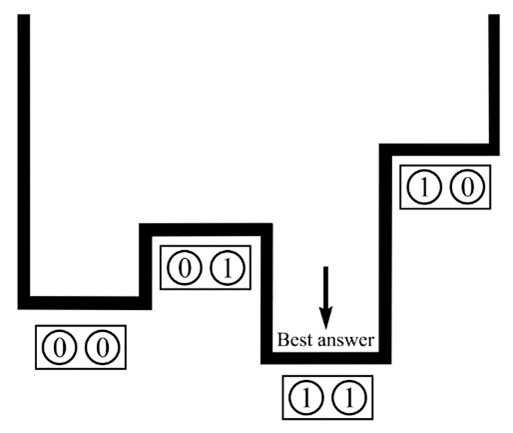
The problem is formulated using the Hamiltonian formalism, which describes an energy operator for the system and aims to find the state with the lowest energy by minimizing the operator.
As I mentioned earlier, there exists an implicit analogy between RBMs, statistical mechanics, and the Boltzmann distribution, making this modeling highly canonical. These concepts are used to model quantum particles in thermal equilibrium states.
However, in this case, the particles are indistinguishable entities, and their energy is discrete, referred to as quantum states of the system and modeled by the Bose-Einstein distribution. An intriguing aspect here is that the Bose-Einstein distribution reduces to the Boltzmann distribution in the classical limit when we model only a few particles.
Let’s draw a vague yet insightful analogy: Each activation of the nodes v and h in the RBM represents the particles of the system, and each configuration of these particles carries an associated energy value, consequently forming a probability distribution. Our objective is to discover an organizing state of these particles that represents the lowest possible energy state.
The advantage of quantum annealers lies in their maturity compared to quantum gate-based systems. They excel in solving a specific class of problems, with commercial distributions of up to 5000 qubits.
How can we leverage Quantum Annealers as an option for Contrastive Divergence?
This part can be quite complex, but I’ll provide some intuition. The first step is to transform the problem into a quantum problem. In the quantum universe, we deal with qubits, represented by particle spins. A spin-up state is denoted by 0, while a spin-down state is denoted by 1. A qubit can exist in a superposition state, so we can represent it as:
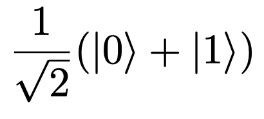
Where the square root of 2 is just some normalization factor. The next step involves converting the NLL into a suitable modeling that incorporates these phenomena, which can be achieved through the Ising model. By employing this model, we can transform the parameters of a system into spins and define the system’s energy based on the NLL function.
As mentioned earlier, the quantum annealer utilizes Hamiltonian modeling. Since we have already converted the NLL into an Ising model, mapping it to the Hamiltonian of a quantum system becomes straightforward. This approach essentially corresponds to solving a Quadratic Unconstrained Binary Optimization (QUBO) problem.
With the Hamiltonian in place, we can input it into the annealer, where all possible spin configurations of the system are explored, and the configuration representing the lowest energy state is determined.
The outcome of this step is a spin configuration that represents the system’s lowest energy state, which then needs to be translated back to the original problem. After performing this translation, we can efficiently obtain samples of h and v from the joint distribution.
To conclude, through sampling, we can calculate the gradient’s value and consequently update the parameters (W, b, a) of the RBM. It’s understandable if you didn’t fully grasp this part, but the key takeaway is that quantum annealers excel at sampling from unknown complex probability distributions, mapping to optimization problems, and finding the ground state.
I hope this example has shed some light on the relationship between RBMs and classical and quantum physics, illustrating a perfect example of how these two realms can converge in a hybrid approach. While we still depend on the classical part, as the quantum annealer handles the sampling of the empirical data distribution, all parameter updates (W, b, a) of the network are conducted through the gradient descent method.
Though there are challenges and approximations involved in this integration, the increasing maturity of quantum annealers and their ability to solve specific problems make them a promising option to advance the field of machine learning and artificial intelligence further. Consequently, we can see a future where the fusion of quantum computing and machine learning leads to remarkable progress in the field of AI.
References
Srivastava, S., Sundararaghavan, V. Generative and discriminative training of Boltzmann machine through quantum annealing. Sci Rep 13, 7889 (2023). https://doi.org/10.1038/s41598-023-34652-4
Perdomo-Ortiz, A., Benedetti, M., Realpe-Gómez, J., & Biswas, R. Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers (2018). IOP Publishing Ltd.
Dixit, V., Selvarajan, R., Alam, M. A., Humble, T. S., & Kais, S. (2021). Training Restricted Boltzmann Machines With a D-Wave Quantum Annealer. Frontiers in Physics, 9, Article 589626. https://doi.org/10.3389/fphy.2021.589626
Slysz, M., Subocz, M., & Kurowski, K. Applying a Quantum Annealing Based Restricted Boltzmann Machine for MNIST Handwritten Digit Classification. (2022) Lecture conducted at Poznan Supercomputing and Networking Center, Poznan, Poland.
.




